The Social Network
Read the Submission Directions
Please submit a PDF using an Rmarkdown file for this task1 both to eCampus and Slack.
First Things First! Download the data set
Please download all of the materials needed for this task.
Idea
The purpose of this task is to analyze the Twitter network of the Members of the U.S. Congress.
Please use the following data files:
congress-twitter-network-edges.csvcontains the edges of this network. Note that unlike in the previous example, these nodes are now directed: they indicate whether the legislator in thesourcecolumn follows the legislator in thetargetcolumn.congress-twitter-network-nodes.csvcontains information about each of the nodes. The only important variables you need to use for this challenge are:id_str(the unique Twitter ID for each legislator; same as in the edge list),name(full name of each legislator),party(Republican, Democrat or Independent), andchamber(repfor the House of Representatives,senfor the Senate).
Task
Please answer the following. Note that this network is too large for us to visualize it directly with R, so let’s try to learn more about it using what we have learned so far.
How many nodes and edges does this network have?
How many components does this network have? As you will see, in this particular case it makes sense that we work only with the giant component.
Who are the most relevant Members of Congress, according to different measures of centrality? Note that this is a directed network, which means there is a difference between indegree and outdegree.
What communities can you find in the network? Use the additional node-level variables to try to identify whether these communities overlap with any of these other attributes. Try different community detection algorithms to see if you get different answers.
Finally, try to visualize the network as well. Instead of plotting it in the Viewer window, you can write directly to a PDF file. I have added a few options here for you so that it’s faster, but note that this will probably take 1-2 minutes.
set.seed(777) fr <- layout_with_fr(g, niter=1000) V(g)$color <- ifelse(V(g)$party=="Republican", "red", "blue") # clue V(g)$shape <- ifelse(V(g)$chamber=="sen", "square", "circle") # clue V(g)$label <- NA V(g)$size <- authority_score(g)$vector * 5 pdf("congress-network.pdf") par(mar=c(0,0,0,0)) plot(g, edge.curved=.25, edge.width=.05, edge.arrow.mode=0) dev.off()
Bonus
Up to this point, we have focused on describing networks, both visually and numerically. Now we turn to trying to explain how networks emerge: what are the mechanisms that explain the structure of the observed networks?
We’ll continue with the example of the Twitter network of Congress. Our goal will be to find the micro-mechanisms that explain following decisions and thus network formation. Now go ahead and load up the following data sets
We’ll continue to use the previous data sets
library(tidyverse)
library(igraph)##
## Attaching package: 'igraph'## The following objects are masked from 'package:dplyr':
##
## as_data_frame, groups, union## The following objects are masked from 'package:purrr':
##
## compose, simplify## The following object is masked from 'package:tidyr':
##
## crossing## The following object is masked from 'package:tibble':
##
## as_data_frame## The following objects are masked from 'package:stats':
##
## decompose, spectrum## The following object is masked from 'package:base':
##
## uniong <- graph_from_data_frame(d=edges,
vertices=nodes,
directed=TRUE)
g <- decompose(g)[[1]]One of the most basic notions governing network formation is homophily, that is, the propensity of individuals to cluster along common traits, such as age, gender, class, etc.
We can measure the extent to which a network is homophilic along a specific variable by computing the assortativity index. Positive values indicate a positive propensity; negative values indicate negative propensity.
assortativity_degree(g, directed=FALSE)## [1] -0.1027231assortativity(g, log(V(g)$followers_count), directed=FALSE)## [1] 0.1064822assortativity_nominal(g, factor(V(g)$chamber))## [1] 0.3989669assortativity_nominal(g, factor(V(g)$party))## [1] 0.6528812assortativity_nominal(g, factor(V(g)$gender))## [1] 0.0830673The main limitation with this approach is that we don’t know to what extent this coefficients are different from what you would find simply by chance in any network. Furthermore, it is hard to disentangle what is the variable that is driving homophily. For example, the proportion of women is higher among Republicans, and thus the homophily result for gender could be simply due to party effects. (Of course, I’m putting aside issues related to causality: homophily could be driven by selection or by social influence.)
prop.table(table(V(g)$gender, V(g)$party), margin=2)##
## Democrat Independent Republican
## F 0.33482143 0.00000000 0.09688581
## M 0.66517857 1.00000000 0.90311419To try to address these limitations, we can rely on exponential random graph models. We will not get into the details, but here’s a general intuition of how these models work:
- These models start from your observed network. It is considered a realization of many possible networks with the same number of nodes and edges.
- The goal is to learn the mechanisms that explain how you get to this specific network, e.g. homophily, reciprocity, transitivity… Each of these mechanisms is considered a parameter in the model.
- Assuming these mechanisms, what is the likelihood of arriving to the network you observe? From the probability distribution of all possible networks based on the parameter space, what is the probability of observing this particular one?
- The goal is to estimate the parameters that best match the observed network using MCMC methods.
For a great introduction to ERGMs, see Robins et al (2007) _An introduction to exponential random graph (p*) models for social networks_, Social Networks.
We can estimate these models with the ergm package in R. Unfortunately, ergm works with object in network format (not igraph), so we will need to convert first between packages using the intergraph package.
library(intergraph)
library(network)## network: Classes for Relational Data
## Version 1.16.1 created on 2020-10-06.
## copyright (c) 2005, Carter T. Butts, University of California-Irvine
## Mark S. Handcock, University of California -- Los Angeles
## David R. Hunter, Penn State University
## Martina Morris, University of Washington
## Skye Bender-deMoll, University of Washington
## For citation information, type citation("network").
## Type help("network-package") to get started.##
## Attaching package: 'network'## The following objects are masked from 'package:igraph':
##
## %c%, %s%, add.edges, add.vertices, delete.edges, delete.vertices,
## get.edge.attribute, get.edges, get.vertex.attribute, is.bipartite,
## is.directed, list.edge.attributes, list.vertex.attributes,
## set.edge.attribute, set.vertex.attributenet <- asNetwork(g)
net## Network attributes:
## vertices = 514
## directed = TRUE
## hyper = FALSE
## loops = FALSE
## multiple = FALSE
## bipartite = FALSE
## total edges= 61766
## missing edges= 0
## non-missing edges= 61766
##
## Vertex attribute names:
## bioid chamber followers_count gender party twitter vertex.names
##
## Edge attribute names not shown(We could also create the object directly as a network object, but converting from igraph is easier.)
What parameters can we add to the model?
edges = number of edges in the network. It’s equivalent to a constant in a regression. Given that this network is relatively sparse, the parameter is negative, which means that the probability of observing any given edge is low. In fact, the estimated parameter in this baseline model is equal to the log of the odds of observing any edge.
library(ergm) reg1 <- ergm(net ~ edges) summary(reg1)## Call: ## ergm(formula = net ~ edges) ## ## Iterations: 5 out of 20 ## ## Monte Carlo MLE Results: ## Estimate Std. Error MCMC % z value Pr(>|z|) ## edges -1.184499 0.004598 0 -257.6 <1e-04 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Null Deviance: 365541 on 263682 degrees of freedom ## Residual Deviance: 287073 on 263681 degrees of freedom ## ## AIC: 287075 BIC: 287085 (Smaller is better.)# no. of edges / ( no. of potential edges - no. of existing edges) log(length(E(g)) / ( length(V(g))*(length(V(g))-1) - length(E(g))))## [1] -1.184499mutual provides rge number of mutual dyads. This parameter captures reciprocity as a mechanism for tie formation. If positive, it means reciprocity is more common than expected given the baseline probability of any two nodes being connected, holding the number of edges constant. In the case below, the positive coefficient means that if you see an edge from
itoj, then you are exp(2.04)=7.76 times more likely to see an edge fromjtoias well.reg2 <- ergm(net ~ edges + mutual)## Starting maximum pseudolikelihood estimation (MPLE):## Evaluating the predictor and response matrix.## Maximizing the pseudolikelihood.## Finished MPLE.## Starting Monte Carlo maximum likelihood estimation (MCMLE):## Iteration 1 of at most 20:## Optimizing with step length 1.## The log-likelihood improved by 0.4038.## Step length converged once. Increasing MCMC sample size.## Iteration 2 of at most 20:## Optimizing with step length 1.## The log-likelihood improved by 2.038.## Step length converged twice. Stopping.## Finished MCMLE.## Evaluating log-likelihood at the estimate. Using 20 bridges: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 . ## This model was fit using MCMC. To examine model diagnostics and check ## for degeneracy, use the mcmc.diagnostics() function.summary(reg2)## Call: ## ergm(formula = net ~ edges + mutual) ## ## Iterations: 2 out of 20 ## ## Monte Carlo MLE Results: ## Estimate Std. Error MCMC % z value Pr(>|z|) ## edges -1.843104 0.006461 2 -285.3 <1e-04 *** ## mutual 2.063706 0.016023 2 128.8 <1e-04 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Null Deviance: 365541 on 263682 degrees of freedom ## Residual Deviance: 268056 on 263680 degrees of freedom ## ## AIC: 268060 BIC: 268081 (Smaller is better.)nodematch captures homophily on a specific factor variable. It measures the increase in the probability that an edge exists between two nodes with the same value on this variable. In the example below, a Member of Congress of the same party is exp(1.50)=4.48 times more likely to follow another Member of Congress if he/she belongs to the same party.
reg3 <- ergm(net ~ edges + mutual + nodematch("party"))## Starting maximum pseudolikelihood estimation (MPLE):## Evaluating the predictor and response matrix.## Maximizing the pseudolikelihood.## Finished MPLE.## Starting Monte Carlo maximum likelihood estimation (MCMLE):## Iteration 1 of at most 20:## Optimizing with step length 1.## The log-likelihood improved by 0.495.## Step length converged once. Increasing MCMC sample size.## Iteration 2 of at most 20:## Optimizing with step length 1.## The log-likelihood improved by 0.2611.## Step length converged twice. Stopping.## Finished MCMLE.## Evaluating log-likelihood at the estimate. Using 20 bridges: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 . ## This model was fit using MCMC. To examine model diagnostics and check ## for degeneracy, use the mcmc.diagnostics() function.summary(reg3)## Call: ## ergm(formula = net ~ edges + mutual + nodematch("party")) ## ## Iterations: 2 out of 20 ## ## Monte Carlo MLE Results: ## Estimate Std. Error MCMC % z value Pr(>|z|) ## edges -2.667315 0.009049 3 -294.8 <1e-04 *** ## mutual 1.594548 0.015154 3 105.2 <1e-04 *** ## nodematch.party 1.531731 0.012008 3 127.6 <1e-04 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Null Deviance: 365541 on 263682 degrees of freedom ## Residual Deviance: 241283 on 263679 degrees of freedom ## ## AIC: 241289 BIC: 241321 (Smaller is better.)nodecov and nodefactor = measure whether individuals with high values on a variable or with a specific value on a factor variable are more likely to follow or to be followed.
absdiff = measures whether individuals with similar values along a continuous variable are more likely to have an edge between them (in either direction).
reg4 <- ergm(net ~ edges + mutual + nodefactor("chamber") + absdiff("followers_count") + nodematch("party") + nodematch("chamber") + nodematch("gender"))## Starting maximum pseudolikelihood estimation (MPLE):## Evaluating the predictor and response matrix.## Maximizing the pseudolikelihood.## Finished MPLE.## Starting Monte Carlo maximum likelihood estimation (MCMLE):## Iteration 1 of at most 20:## Optimizing with step length 0.493132739919402.## The log-likelihood improved by 2.453.## Iteration 2 of at most 20:## Optimizing with step length 0.677091744669799.## The log-likelihood improved by 1.965.## Iteration 3 of at most 20:## Optimizing with step length 0.181386433493612.## The log-likelihood improved by 1.699.## Iteration 4 of at most 20:## Optimizing with step length 0.301266888230387.## The log-likelihood improved by 2.284.## Iteration 5 of at most 20:## Optimizing with step length 0.486530464584912.## The log-likelihood improved by 1.224.## Iteration 6 of at most 20:## Optimizing with step length 0.183981626536171.## The log-likelihood improved by 1.915.## Iteration 7 of at most 20:## Optimizing with step length 0.542894308311544.## The log-likelihood improved by 2.439.## Iteration 8 of at most 20:## Optimizing with step length 0.500898012508401.## The log-likelihood improved by 1.86.## Iteration 9 of at most 20:## Optimizing with step length 0.189330764485591.## The log-likelihood improved by 1.534.## Iteration 10 of at most 20:## Optimizing with step length 0.500131152024041.## The log-likelihood improved by 2.567.## Iteration 11 of at most 20:## Optimizing with step length 0.224774143629235.## The log-likelihood improved by 1.276.## Iteration 12 of at most 20:## Optimizing with step length 0.448698584132466.## The log-likelihood improved by 2.844.## Iteration 13 of at most 20:## Optimizing with step length 0.296806119132533.## The log-likelihood improved by 2.002.## Iteration 14 of at most 20:## Optimizing with step length 0.112004858017235.## The log-likelihood improved by 2.318.## Iteration 15 of at most 20:## Optimizing with step length 0.251976978490044.## The log-likelihood improved by 1.29.## Iteration 16 of at most 20:## Optimizing with step length 0.55745627541811.## The log-likelihood improved by 2.498.## Iteration 17 of at most 20:## Optimizing with step length 0.469147681779228.## The log-likelihood improved by 1.987.## Iteration 18 of at most 20:## Optimizing with step length 0.259454699669255.## The log-likelihood improved by 2.629.## Iteration 19 of at most 20:## Optimizing with step length 0.269197838244846.## The log-likelihood improved by 2.626.## Iteration 20 of at most 20:## Optimizing with step length 0.505250894347924.## The log-likelihood improved by 3.469.## MCMLE estimation did not converge after 20 iterations. The estimated coefficients may not be accurate. Estimation may be resumed by passing the coefficients as initial values; see 'init' under ?control.ergm for details.## Finished MCMLE.## Evaluating log-likelihood at the estimate. Using 20 bridges: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 . ## This model was fit using MCMC. To examine model diagnostics and check ## for degeneracy, use the mcmc.diagnostics() function.summary(reg4)## Call: ## ergm(formula = net ~ edges + mutual + nodefactor("chamber") + ## absdiff("followers_count") + nodematch("party") + nodematch("chamber") + ## nodematch("gender")) ## ## Iterations: 20 out of 20 ## ## Monte Carlo MLE Results: ## Estimate Std. Error MCMC % z value Pr(>|z|) ## edges -3.719e+00 7.577e-03 100 -490.83 <1e-04 *** ## mutual 1.360e+00 6.721e-03 100 202.35 <1e-04 *** ## nodefactor.chamber.sen 4.255e-01 5.342e-03 100 79.66 <1e-04 *** ## absdiff.followers_count 2.996e-07 2.338e-08 17 12.81 <1e-04 *** ## nodematch.party 1.636e+00 3.698e-03 100 442.51 <1e-04 *** ## nodematch.chamber 1.350e+00 6.555e-03 100 205.98 <1e-04 *** ## nodematch.gender -1.769e-01 4.437e-03 100 -39.86 <1e-04 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Null Deviance: 365541 on 263682 degrees of freedom ## Residual Deviance: 231646 on 263675 degrees of freedom ## ## AIC: 231660 BIC: 231734 (Smaller is better.)
One practical issues with ERGMs is that when you add multiple variables, the MCMC chains often have convergence issues. Sometimes just running these for more iterations and increasing the thinning parameter will fix this. Sadly, very often it’s more difficult than that…
mcmc.diagnostics(reg2)## Sample statistics summary:
##
## Iterations = 16384:4209664
## Thinning interval = 1024
## Number of chains = 1
## Sample size per chain = 4096
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## edges -342.5 228.9 3.577 59.85
## mutual -186.5 92.4 1.444 24.57
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## edges -746.0 -510 -344.5 -187.8 175.6
## mutual -369.6 -252 -185.0 -121.0 -13.0
##
##
## Sample statistics cross-correlations:
## edges mutual
## edges 1.0000000 0.7242037
## mutual 0.7242037 1.0000000
##
## Sample statistics auto-correlation:
## Chain 1
## edges mutual
## Lag 0 1.0000000 1.0000000
## Lag 1024 0.9928789 0.9931975
## Lag 2048 0.9860376 0.9864289
## Lag 3072 0.9793953 0.9793711
## Lag 4096 0.9726075 0.9724758
## Lag 5120 0.9662138 0.9659111
##
## Sample statistics burn-in diagnostic (Geweke):
## Chain 1
##
## Fraction in 1st window = 0.1
## Fraction in 2nd window = 0.5
##
## edges mutual
## 1.288 2.103
##
## Individual P-values (lower = worse):
## edges mutual
## 0.19766352 0.03546197
## Joint P-value (lower = worse): 0.5816436 .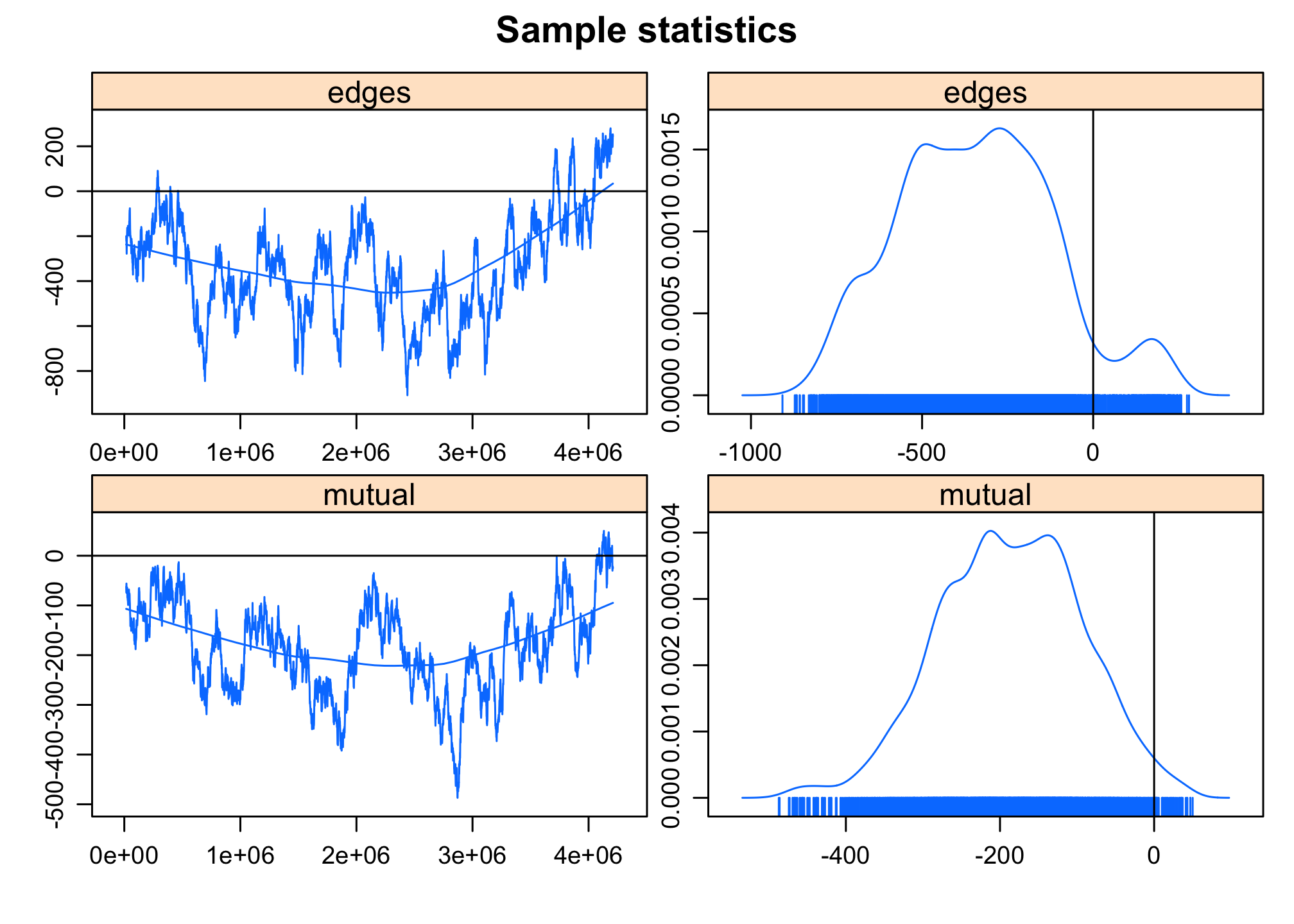
##
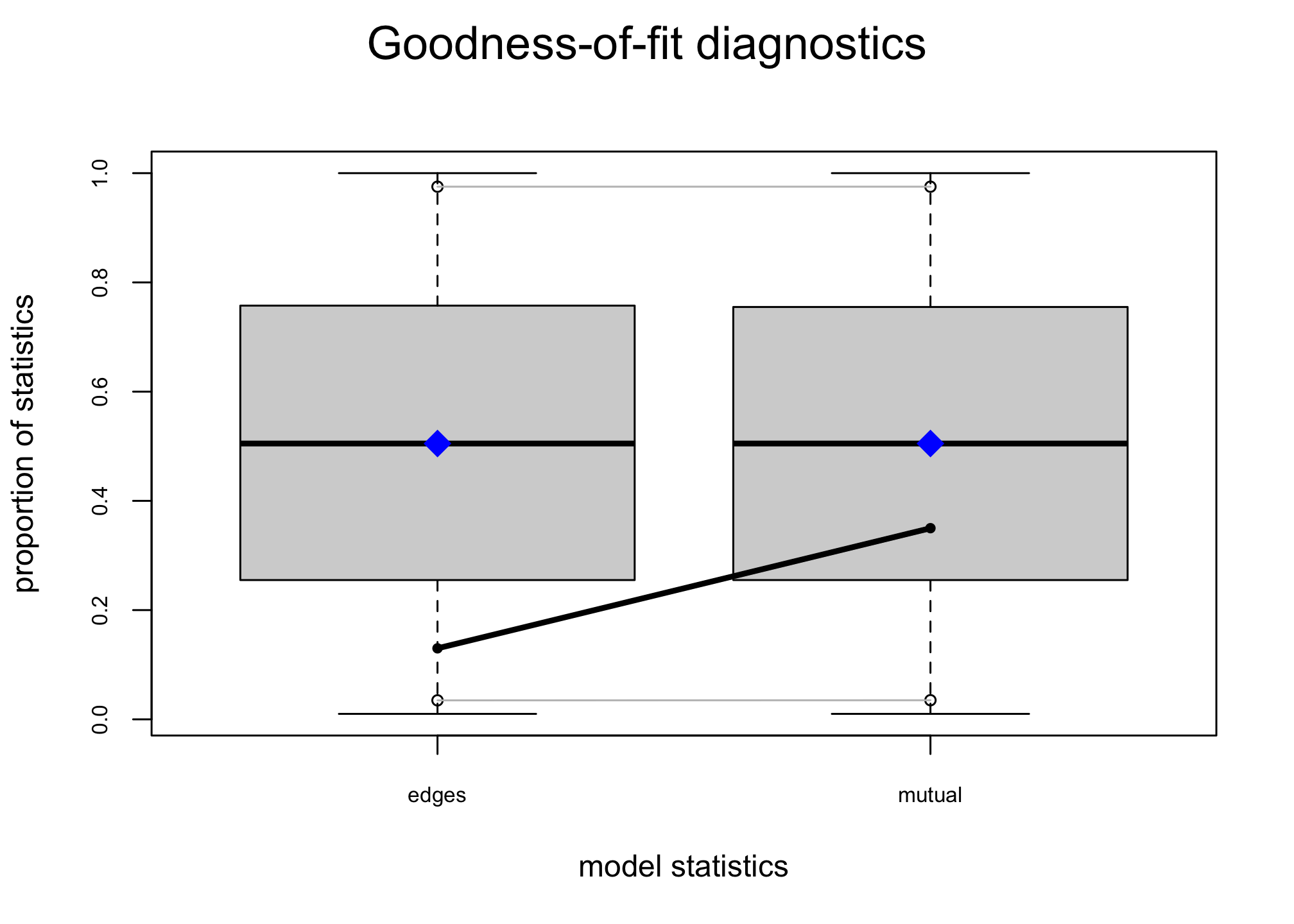
## MCMC diagnostics shown here are from the last round of simulation, prior to computation of final parameter estimates. Because the final estimates are refinements of those used for this simulation run, these diagnostics may understate model performance. To directly assess the performance of the final model on in-model statistics, please use the GOF command: gof(ergmFitObject, GOF=~model).Another way to check the results of the model is to simulate networks assuming the estimated parameters and compare their degree distribution to the observed indegree distribution. (Warning: running the code below will take a while!)
sims <- simulate(reg2, nsim=10)
summary(sims)## Number of Networks: 10
## Model: net ~ edges + mutual
## Reference: ~Bernoulli
## Constraints: ~.
## Parameters:
## edges mutual
## -1.843104 2.063706
##
## Stored network statistics:
## edges mutual
## [1,] 61990 17048
## [2,] 61974 17060
## [3,] 61992 17051
## [4,] 61991 17047
## [5,] 61975 17045
## [6,] 61948 17050
## [7,] 61951 17047
## [8,] 61959 17042
## [9,] 61941 17033
## [10,] 61950 17048
## attr(,"monitored")
## [1] FALSE FALSE## Number of Networks: 10
## Model: net ~ edges + mutual
## Reference: ~Bernoulli
## Constraints: ~.
## Parameters:
## edges mutual
## -1.843104 2.063706reggof <- gof(reg2 ~ idegree)
plot(reggof)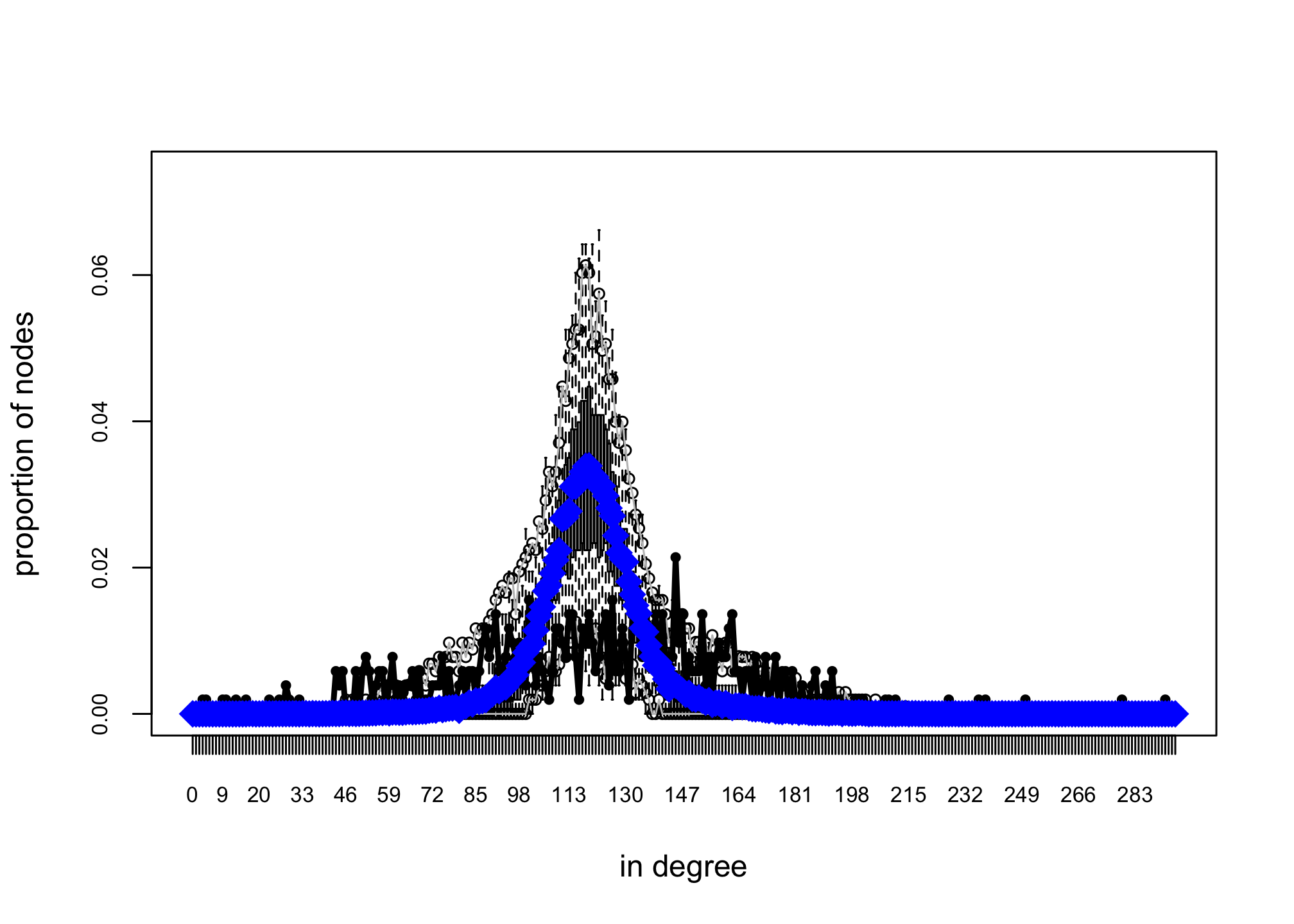
In this challenge you will work with a dataset about classroom interactions. The goal is to understand the extent to which homophily explains friendships across students.
First, let’s load the dataset, which is available in the NetData package.
library(NetData)
data(studentnets.ergm173)
str(nodes)## 'data.frame': 22 obs. of 5 variables:
## $ std_id : int 104456 113211 114144 114992 118466 118680 122713 122714 122723 125522 ...
## $ gnd : int 2 2 1 1 1 2 2 1 1 1 ...
## $ grd : int 10 10 10 10 10 10 10 10 10 10 ...
## $ rce : int 4 1 4 4 2 4 4 1 4 4 ...
## $ per_cap_inc: int 4342 13452 13799 13138 8387 9392 12471 10391 17524 12145 ...str(edges)## 'data.frame': 160 obs. of 5 variables:
## $ ego_id : int 104456 104456 104456 104456 104456 104456 104456 104456 104456 104456 ...
## $ alter_id : int 104456 114992 118680 122713 122723 125522 126101 126784 132942 138966 ...
## $ sem1_friend : int 0 0 0 0 0 1 0 0 0 0 ...
## $ sem2_friend : int 1 1 1 1 1 1 1 1 1 1 ...
## $ sem1_wtd_dicht_seat: int 0 0 0 0 1 0 0 0 1 1 ...You can read the codebook by typing: ?NetData::nodes
The student-level variables are:
std_id: student IDgnd: gender (1 = male, 2 = female)grd: grade (always 10th)rce: race (1 = Hispanic, 2 = Asian, 3 = African-American, 4 = White)per_cap_inc: per capita income from the 1990 census
The edge-level variables are:
ego_idandalter_idare the source and target of the edgesem1_friendsandsem2_friendsindicate responses to friendship survey in semesters 1 and 2(0 = not friends, 1 = friend, 2 = best friends)sem1_wtd_dicht_seatindicates whether students were seating next to each other
Our goal will be to explain friendships in the first semester, so we will keep only edges where sem1_friends>0.
some_edges <- edges[edges$sem1_friend>0,]- First create the igraph object
Here you will get an error. Why? Some students name as friends other students in different classrooms. We’ll get rid of those edges and try again. How many nodes and edges does this network have? Visualize it to see what else you learn.
edges <- edges[edges$alter_id %in% nodes$std_id,]- Convert the
igraphobject tonetworkformat. Check that the size of the network is the same as before.
And now we’re ready to start estimating models!
Estimate a baseline model with total number of edges and number of mutual edges. What do you learn?
Examine the effect of similarity across race, gender, and income. What do you learn?
:::
If you use an external file for your data, please submit that as well.↩︎